Le Billard intermittent

Règles du jeu

On choisi un rectangle de taille x*y
On part d'un des points présent sur sa circonférence.
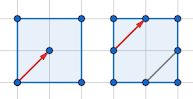
On trace la diagonale unitaire avec un angle de 45°
On continue comme cela en traçant une diagonale sur deux.
Lorsqu'on arrive contre un bord, on "rebondit" comme au billard.
On s'arrête de dessiner les diagonales dans deux cas :

• Lorsqu'on arrive à un angle du rectangle,
• Lorsque la diagonale a déjà été dessinée.

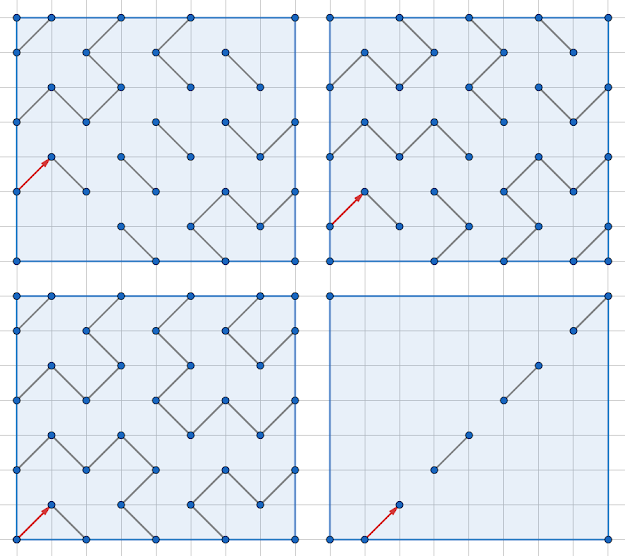
Exemple avec un rectangle 7*8 en commençant à un des angles

Une pensée pour Roger, Robin et Le Myriogon pour cette découverte !

Pour ne pas "spoiler", je vous ai mis un petit tableau de synthèse en bas de page...

Les différents cas pour les rectangles  x*y

Le cas du x*1
Le cas du x*2
Le cas du x*3
Le cas du x*4
Le cas du x*5
Le cas du x*6
Le cas du x*7
Le cas du x*8
Le cas du x*9

Le cas du x*10

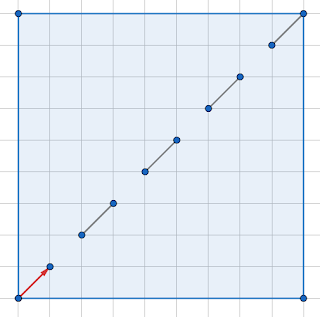
Le cas du x*1 [haut]

Il n'y a qu'une seule solution possible

Les cas du x*2 [haut]

Le 1*2

Il y a 2 solutions, bien que symétriquement identiques.

Le 2*2

Il y a 2 solutions, différentes.

Les cas du x*3 [haut]

Le 1*3

3 solutions différentes. On commence à distinguer que les x*1 seront "hachurés" tout ou partiellement.

Le 2*3

3 solutions totalement différentes

Le 3*3

2 symétriques et 1 différente des 2 premières

Les cas du x*4 [haut]

Le 1*4

4 cas de hachures

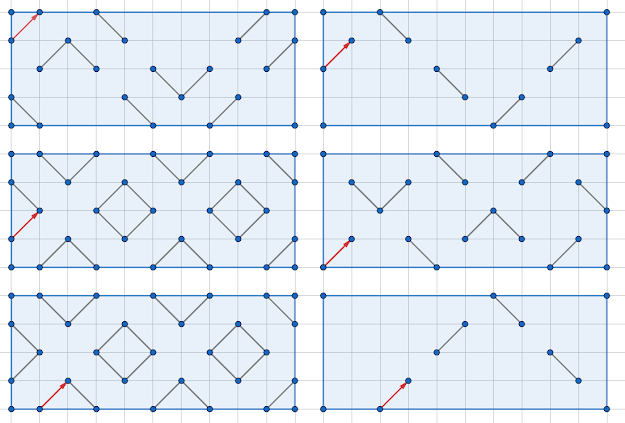
Le 2*4

5 solutions dont 2 identiques, 1 symétrique et 2 différentes

Le 3*4

2 symétriques et 4 autres différentes

Le 4*4

4 différentes

Les cas du x*5 [haut]

Le 1*5

5 hachurées différemment

Le 2*5

6 différentes

Le 3*5

7 différentes

Le 4*5

8 solutions

Le 5*5

5 solutions

Les cas du x*6 [haut]

Le 1*6

6 solutions

Le 2*6

7 solutions

Le 3*6

8 solutions

Le 4*6

9 solutions

Le 5*6

10 solutions

Le 6*6

6 solutions

Les cas du x*7 [haut]

Le 1*7

7 solutions

Le 2*7

8 solutions

Le 3*7

9 solutions

Le 4*7

10 solutions

Le 5*7

11 solutions

Le 6*7

12 solutions

Le 7*7

7 solutions

Les cas du x*8 [haut]

Le 1*8

8 solutions

Le 2*8

9 solutions

Le 3*8

10 solutions

Le 4*8

11 solutions

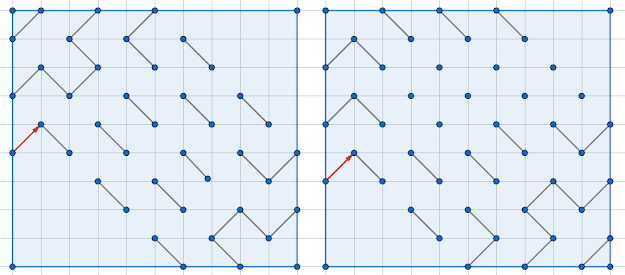
Le 5*8

12 solutions

Le 6*8

13 solutions

Le 7*8

14 solutions

Le 8*8

8 solutions

Les cas du x*9 [haut]

Le 1*9

Le 2*9

Le 3*9

Le 4*9

Le 5*9

Le 6*9

Le 7*9

Le 8*9

Le 9/9

Les cas du x*10 [haut]

Le 1*10

Le 2*10

Le 3*10

Le 4*10

Le 5*10

Le 6*10

Le 7*10

Le 8*10

Le 9*10

Le 10*10

Tableaux de relevé [haut]

Voici le nombre de cas possibles par rectangle :

Voici quelques conjectures sur le nombre de cas possibles par rectangle :

1. S'il s'agit d'un carré de coté x, le nombre de cas sera de x ;
2. Pour un rectangle x*y ou x est différent de y, le nombre de cas sera x + y - 1.

J'ai dénombré ensuite les "pavages fermés". 

En considérant qu'un pavage fermé est reconnaissable par le fait que la diagonale est toujours reliée à une autre sauf aux bords du rectangle.

Je peux faire clairement quelques conjectures :

1. Un carré n'a jamais de pavage fermé en dehors du 2*2
2. Un rectangle x*y où x = y - 1  a toujours un seul pavage fermé
3. Un rectangle x*y où x = y - 2 et x et y sont pairs auront y-1 pavages fermés
4. Un rectangle x*y où x ou y sont impairs n'auront jamais plus de 1 pavage fermé

J'ai ensuite dénombré le nombre de cas contenant un petit carré :

Inutile de préciser que je n'ai pas de conjecture intéressante. Il faudrait probablement sortir le tableau pour les cas allant jusqu'à 20*20 par exemple :-(

N'hésitez pas à mettre dans les commentaires d'autres conjectures que vous auriez identifiées.